SUMMARY
When using Multi Body Dynamics (MBD), it’s important to set up a model that doesn’t take too long time to solve. Using rigid bodies is the best approach to achieve this. In Ansys Motion, when some flexible parts are necessary, there are two options to calculate stress in bodies: The Nodal approach, which utilizes full Finite Element formulation, and the Modal approach, employing a modal linear expansion. This blog compares these two methodologies to establish differences in stress results.
Modal and Nodal analysis.
Using Nodal approach the solver will perform full FEA calculation, involving the maximum Degrees of Freedom (DOF) and matrix size within the model. On the other hand, the modal approach assumes the deformation vector u is represented by linearly combining a set of mode shapes.
The scale factors or amplitudes a are called modal coordinates and Ψ is a set of mode shapes.
We can see that a deformation can be built as:
Then, the solver will first calculate modal analysis for flexible parts and will use the calculated modes to solve the model. In this case the number of DOF will be reduced considerably. This methodology is applicable exclusively to linear models.
Motion model.
In this example, a hydraulic excavator assembly has been simulated using various joints and motion functions to replicate hydraulic actuators. A load is applied to the bucket to simulate the weight it carries. The model is solved using different approaches. Initially, rigid bodies are employed to establish a base solving time. Subsequently, a second model involves 5 flexible bodies using a nodal approach. Finally, the last model also utilizes flexible bodies but employs a modal solution instead of full FEA nodal calculations.
For the Rigid body model, the calculation time is under one second. However, this model doesn't yield any stress or strain results.
When employing the Nodal approach, there are more than 47k DOF’s and 271 sec to obtain a solution.
Using Modal flexible bodies, the analysis has around 200 DOF’s and takes around 5 sec. This is an important difference with full FEA calculations.
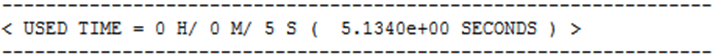
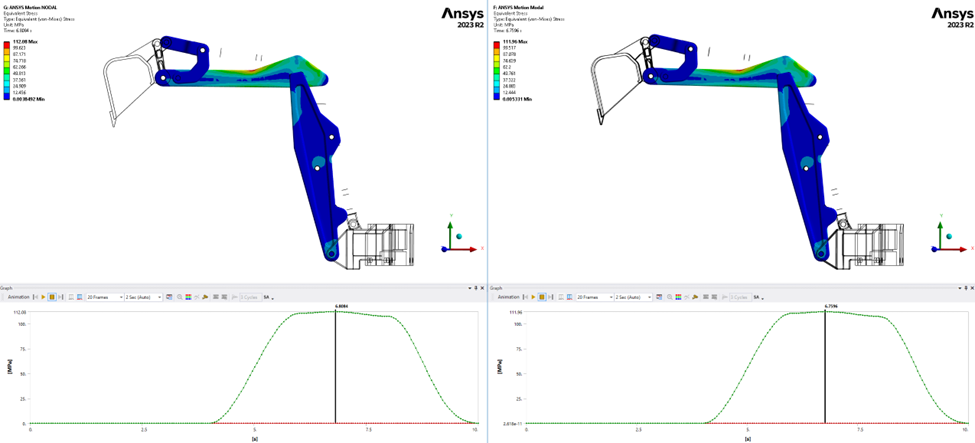
Stress results.
The equivalent stress during the different time steps is essentially the same in both models. The maximum value reached for the Nodal model (right side) is 112.08MPa at 6.80 sec and for the Modal is 111.96 at 6.72 sec. Stress difference is 0.107%.
ADDITIONAL REMARKS
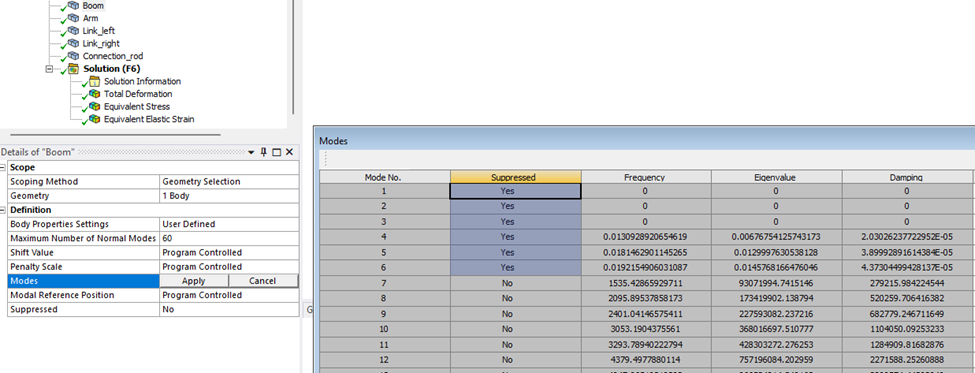
You can control the maximum number of modes used for each body modal expansion and see how the first mode shapes are suppressed to improve solution’s quality.
RECOMMENDATIONS
Is not possible to use nonlinear materials for Modal bodies. It is important to use this technique only where small deformations and linear material assumptions apply.
CONCLUSIONS
The Modal body approach is useful for quickly finding solutions and verifying general stress states. Once it's determined if linear materials are applicable in each specific case, users can switch to Nodal analysis if needed.
The time saved using this method can be crucial during the preliminary design phase. Users can test various scenarios and then transition to a full nodal model once they've identified the most promising ones.