SUMMARY
One of the most well-known challenges in structural simulation lies in achieving a balance between accuracy and computational effort. Bolt thread modeling serves as a notable example, wherein there is a need to precisely understand the stress distribution around the thread. However, the computational cost often compels us to resort to oversimplifications to ensure the feasibility of the simulation. In this blog, we will explore Contact Geometry Correction, a comprehensive approach to effectively reconcile these competing demands.
CONTACT GEOMETRY CORRECTION.
In Ansys Mechanical Contacts, several properties can be utilized to enhance contact performance. Among them, the ‘Contact Geometry Correction’ offers two options: ‘Smoothing’ for circular and revolution geometries and ‘Bolt Thread’.
We are specifically employing the 'Bolt Thread' option to gain a more comprehensive understanding of stresses without the need to model the geometric details of the actual threads. The simplified model is capable of modeling with the near accuracy of a true threaded-bolt model based on internally performed calculations to approximate the behavior of the bolts. This technique is applicable in both 2D axisymmetric and 3D models, using smooth cylindrical surfaces for the bolt and the nut. It is compatible with various types, including No Separation, Frictionless, Rough, and Frictional. Asymmetric behavior must be explicitly defined.
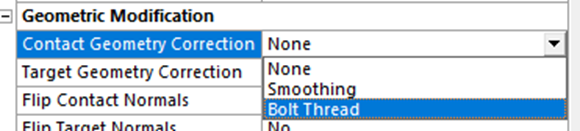
To define this, it’s necessary to specify some thread and axis of revolution information, most of them are self-explanatory. The mean pitch diameter can be found in standard bolt dimension charts:
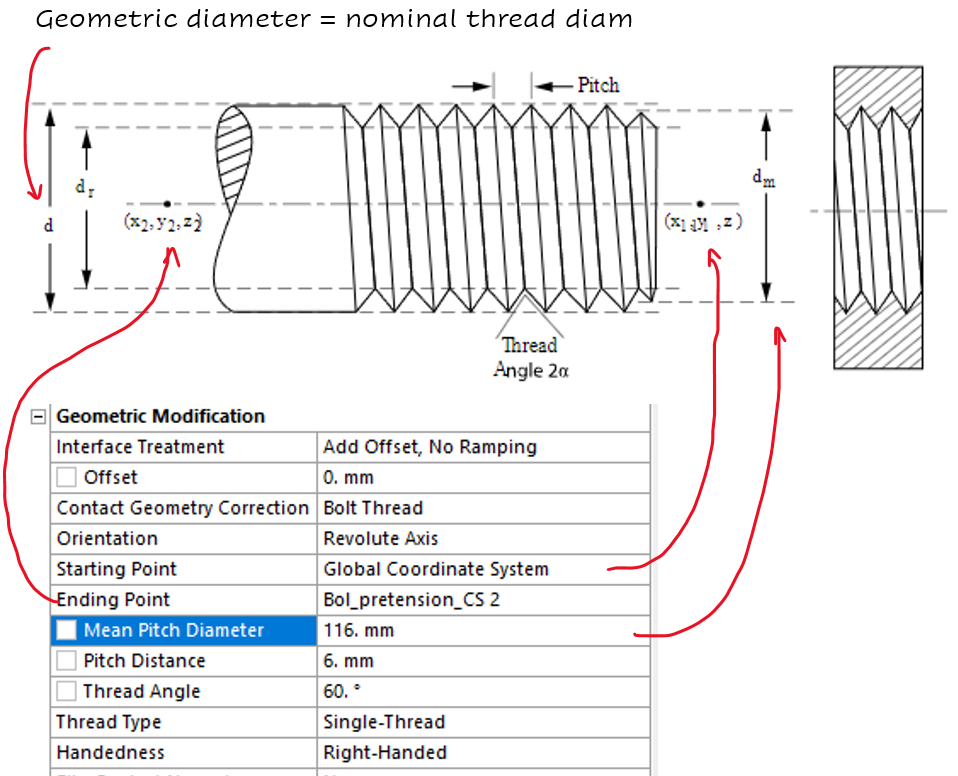
EXAMPLE.
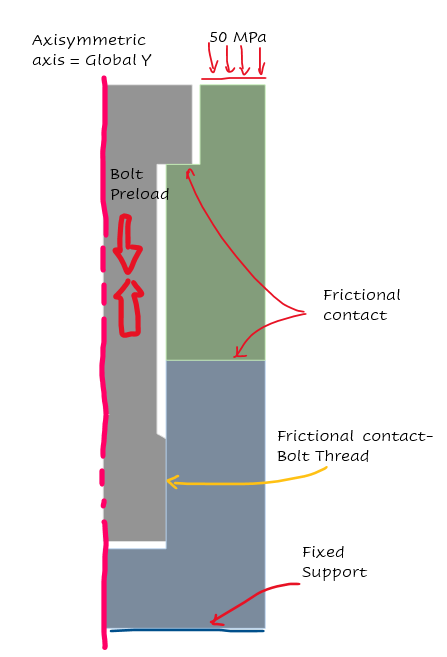
A 2D Axisymmetric model was established to demonstrate the functioning of this technique. The model comprises a single 120 mm bolt subjected to an axial preload of 2544690N applied during the initial timestep. There are three frictional contact zones: two 'Classic contacts' between the two plates and the other between the Bolt head and the upper plate, the third simplified contact is implemented to simulate the threaded connection. For all contacts, a friction coefficient of 0.15 was specified. Additionally, a fixed support at the bottom line was employed to constrain the model. In the subsequent timestep, a 50 MPa pressure was applied to the upper line to represent the structural load and assist in alleviating tension in the bolt shank.
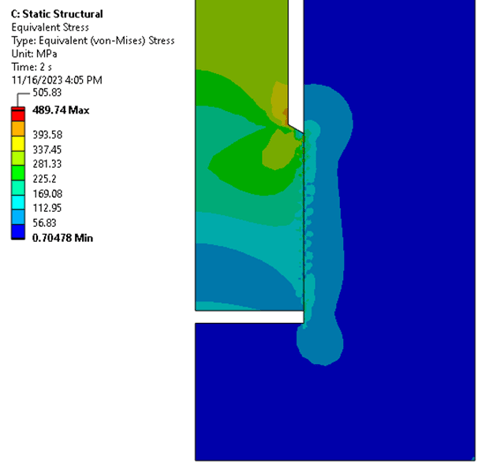
RESULTS.
After solving the model, stress contours in the contact zone mimicking a threaded geometry become visible. This aspect provides confidence in the effectiveness of this technique.
But how good is this approach? The only way to determine its efficacy is by comparing these results with those from a fully detailed geometric simulation. In this second model everything is set up similarly incorporating threaded geometry and utilizing classic Frictional contact.
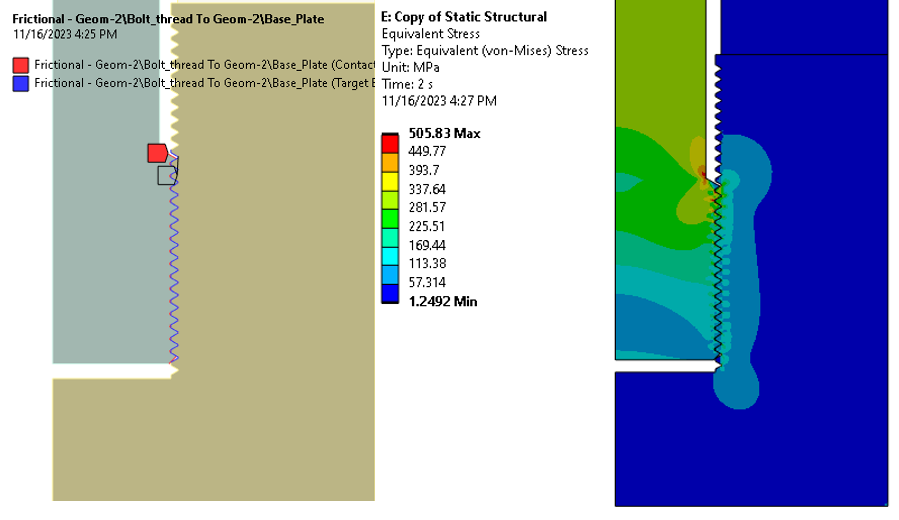
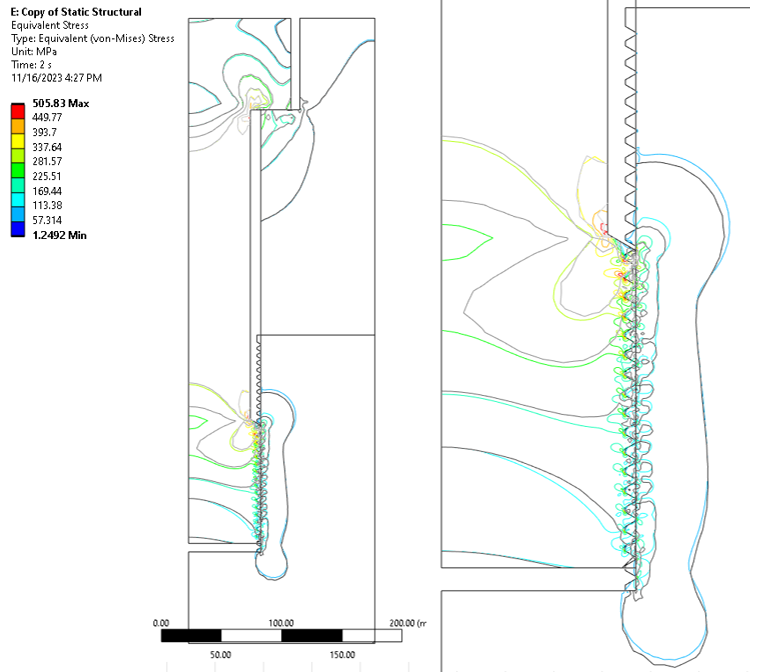
The following image provides a detailed examination of stress contours. Isolines and equal stress scales are employed, where grayscale lines correspond to the simplified contact model, while the rainbow-colored lines represent data from the fully detailed model. The likeness is quite striking.
Comparing the mesh counting and solve time highlights the advantages in resources consumption of this technique:

RECOMMENDATIONS.
Is important to make some refinement in the threaded zone. The element size should be less than the Pitch distance to obtain more accurate results.
The bolt surface should be the contact side and the contact behavior as Asymmetric.
The Axis points, defined in this example as coordinate systems should be in the appropriate geometric bolt axis.
CONCLUSION.
This technique is particularly appealing when the stress distribution near the threaded zone is not the primary focus of the simulation. Additionally, its use of less refined mesh and reduced solving time makes it a favorable option to consider in simulation planning.
NOTE:
Remember Axisymmetric models must be in XY plane, and its rotational axis is Y.
Nov 20, 2023 6:27:06 AM
