RF designers rely on HFSS to design, optimize, and debug their projects. Optimization is essential but often computationally costly. Choosing the right optimizer is critical—especially when the model has many variables, wide ranges, and aggressive targets. Before launching a full optimization, engineers may explore the design space—for example, enabling HFSS’s derivative post-processing to narrow down the parameters that matter most.
Below we summarize the optimizers available in HFSS. Some are gradient-based; others use stochastic/heuristic search. The first table identifies each optimizer’s search method (gradient vs. non-gradient) and gives a relative speed indication.
| Search Type | Gradient-Based? | Continuous / Discrete Support | Speed | |
| Screening (Search-based) | Direct Sampling | No | Continuous & Discrete | Very Fast |
| Pattern Search (Search-based) | Derivative-free | No | Continuous + Discrete | Moderate |
| Multi-Objective Genetic Algorithm (Random-search) | Evolutionary | No | Continuous & Discrete | Slow |
| Adaptive Multiple-Objective (Random Search) | Evolutionary | No | Continuous & Discrete | Slow |
| Genetic Algorithm (Random Search) | Evolutionary | No | Continuous & Discrete | Slow |
| Nonlinear Programming by Quadratic Lagrangian (Gradient) | Gradient-based | Yes | Continuous | Fast |
| Mixed-Integer Sequential Quadratic Programming (Gradient & Discrete) | Hybrid | Yes | Continuous + Discrete | Moderate |
| Adaptive Single-Objective (Gradient) | Adaptive Gradient | Yes | Continuous | Moderate |
| Sequential Nonlinear Programming (Gradient) | Gradient-based | Yes | Continuous | Fast |
| Sequential Mixed Integer Nonlinear Programming (Gradient & Discrete) | Hybrid | Yes | Continuous + Discrete | Moderate |
| Quasi-Newton (Gradient) | Gradient-based | Yes | Continuous | Fast |
| MATLAB | External | Depends | Depends | Depends |
The next table details each technique and its ideal use cases. Some excel with a single objective or a small set of variables, while others are better suited to complex or multi-constraint goals.
| Best For | Notes / Characteristics | |
| Screening (Search-based) | Similar to derivatives. Used to find rough parameter trends before performing intensive optimization. Good for via breakouts, complex devices, and manufacturing tolerance studies (similar to statistical analysis). |
Uses uniform sampling with no refinement; helps identify the most sensitive parameters. |
| Pattern Search (Search-based) | For non-smooth problems with few variables. Useful after applying other types of optimizers. Example: shifting an antenna resonance to a specific frequency |
Explores the parameter space through pattern expansion and contraction. |
| Multi-Objective Genetic Algorithm (Random-search) (MOGA) | For complex, non-convex, multi-objective designs involving multiple conflicting goals. Best used when objectives have different weights. Good for filters as well as array antennas. |
Simulates natural evolution (selection, crossover, mutation); robust against local minima. Starts with an initial population and gradually converges. Handles nonlinear relationships between goals and variables. |
| Adaptive Multiple-Objective (Random Search) (AMO) | For multi-objective trade-offs (e.g., gain vs. bandwidth). Ideal for phased-array antennas with tight tolerances, large PCB models, and designs with many variables. | Builds Pareto fronts to balance exploration and exploitation. Does not use gradient information and relies on a smaller number of solutions. |
| Genetic Algorithm (Random Search) (GA) | For nonlinear, discontinuous objectives. Best suited for single antennas, simple goals, and single-objective problems. | Robust to local minima. Weaker overall performance but converges quickly to a local minimum. |
| Nonlinear Programming by Quadratic Lagrangian (Gradient) (NPQL) | For smooth, differentiable problems. Used for final design tuning or as a follow-up after a random search technique such as MOGA.Best for a small number of variables or when one objective dominates. | Uses Lagrange multipliers and quadratic subproblems; may fail with discontinuities. After each iteration, the program approximates the goal with a quadratic function. Can get stuck in a local minimum. |
| Mixed-Integer Sequential Quadratic Programming (Gradient & Discrete) (MISQP) | For mixed-variable designs (geometry + on/off options). Useful for antenna array design, filter design, and simple PCB trace optimization. Typically run before search-pattern techniques and after random-search techniques. | Combines iterative gradient methods with integer-variable handling. Initially uses continuous values, then iterates by creating branches of searches. |
| Sequential Mixed Integer Nonlinear Programming (Gradient & Discrete) (SMINP) | For mixed topologies; similar to MISQP but used with nonlinear objectives. | Allows partial handling of discrete (integer) parameters. |
| Adaptive Single-Objective (Gradient) | Single-goal, smooth problems | Adjusts step size adaptively; converges faster than basic gradient |
| Sequential Nonlinear Programming (Gradient) | Smooth, single-objective problems | Classic constrained optimization; sensitive to initial guess |
| Quasi-Newton (Gradient) | Convex, differentiable problems | Approximates Hessian matrix; faster convergence than basic gradient |
| MATLAB | Custom algorithms | Allows you to call MATLAB optimization functions if installed |
The final table guides RF designers in choosing an optimizer based on the objective. For PCB and many antenna problems, gradient-based methods are usually preferred; for filter design, quasi-random search tends to work best.
| Design Type | Recommended Optimizer |
| Smooth & continuous | Quasi-Newton or Sequential Nonlinear Programming |
| Contains discrete variables | Mixed-Integer SQP or Pattern Search |
| Multiple conflicting goals (e.g., Gain vs Bandwidth) | Multi-Objective Genetic Algorithm or Adaptive Multiple-Objective |
| Discontinuous response (HFSS field jumps, mesh changes) | Genetic Algorithm or Pattern Search |
| Quick exploration / initial screening | Screening |
| Custom / advanced control | MATLAB interface |
For each type, there are parameters that the user can control
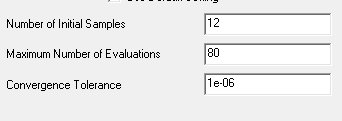
Screening: Number of samples.
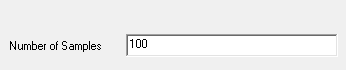
Pattern Search: number of iterations
Multi-objective genetic algorithm
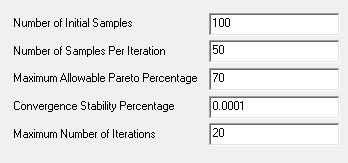
Adaptive multiple-objective
Genetic algorithm
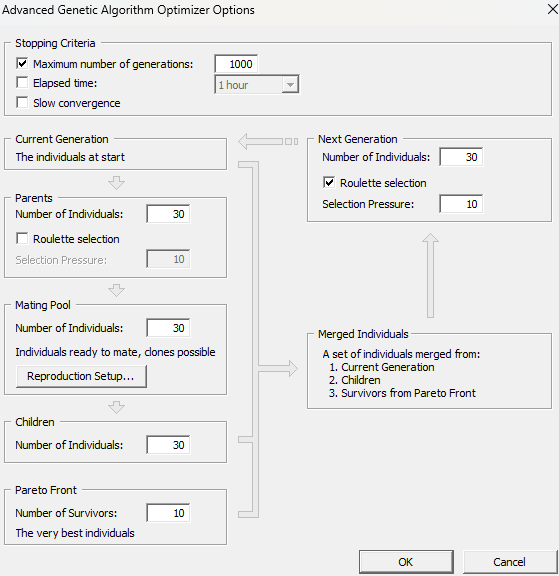
Non-linear programming by quadratic Lagrangian: Select between forward and center.
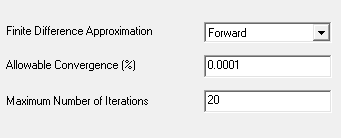
Mixed-Integer sequential quadratic programming.
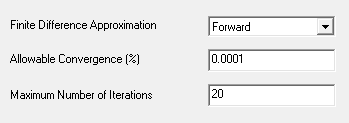
Adaptive single-objective.
Sequential nonlinear programming: Number of iterations.
Sequential mixed integer nonlinear programming: Number of iterations.
Quasi-Newton: Number of iterations.
Ozen Engineering Expertise
Ozen Engineering Inc. leverages its extensive consulting expertise in CFD, FEA, optics, photonics, and electromagnetic simulations to achieve exceptional results across various engineering projects, addressing complex challenges like multiphase flows, erosion modeling, and channel flows using Ansys software.
We offer support, mentoring, and consulting services to enhance the performance and reliability of your systems. Trust our proven track record to accelerate projects, optimize performance, and deliver high-quality, cost-effective results for both new and existing water control systems. For more information, please visit https://ozeninc.com.
Suggested blogs
