Summary
In Part 1 of this series, we described how to determine analysis duration and the number of time steps required to achieve accurate transient structural analysis results simulating the impact of a flexible cylindrical rod with a rigid surface, as well as verifying compliance to various hand calculations based on energy methods. Part 2 of this series focuses on this same geometry while it impacts with another more flexible object. In this case, being a flat plate. We explore further how to define the transient structural duration and number of time-steps based on the flexibility of both of these components and explore and discuss how we can expect results to change depending on whether we choose to establish our time-step sizing based on the more rigid, or the more flexible of these two components. Read below to better understand these topics and more.
Details
In Part 1, we started with our first example which explored the drop of a cylindrical bar on to a hard surface. The bar had a diameter of 25.4 mm and a length of 254 mm and mass density of 7.85e-06 [kg/mm³]. This bar was dropped from 1 meter from the bottom face.
The second model we use in Part 2 contains our shaft geometry, but now, instead of impacting a rigid surface, it impacts a more flexible plate. The impacted plate is 254x254mm and is 5mm thick. It is made from the same material as the shaft and the shaft bottom face has contact defined with the plate top face. We will need to calculate the stiffness of the plate in the impact direction. To do this, we will simply support all edges around the plate and apply a 9.9079 N load to the top of the shaft and calculate the maximum deflection of the plate.
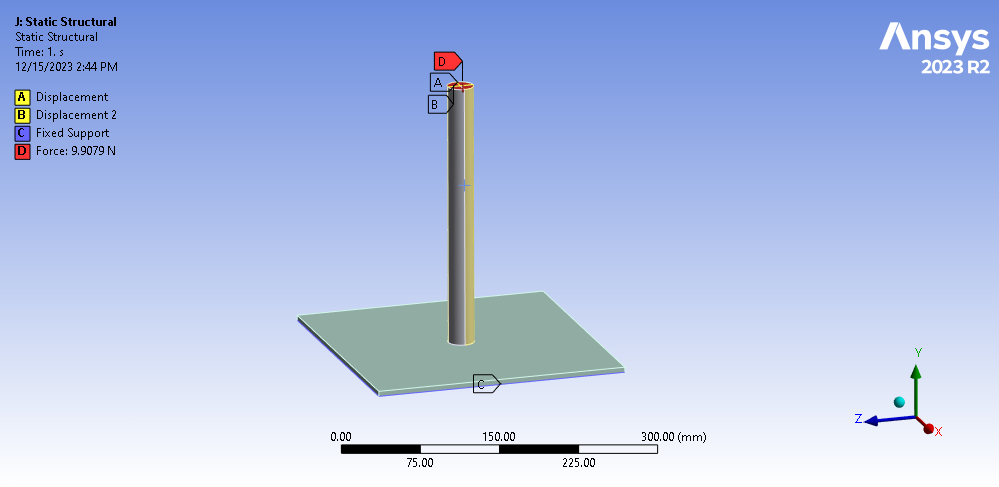
Figure 1: Cylindrical Rod and Flat Plate Geometry
The deflections are as follows:
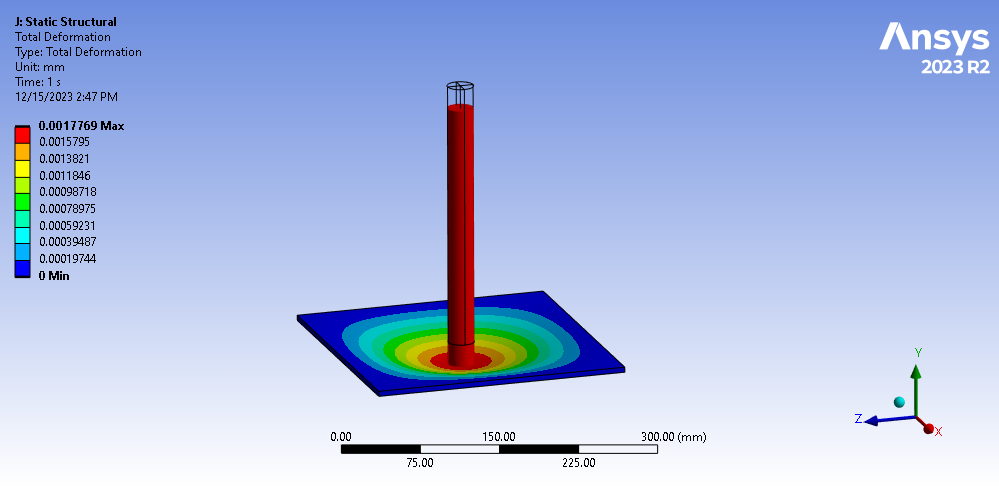
Figure 2: Static Structural Deflection Results
Specifically, we want the average Y-direction deflection on the plate immediately under the rod.
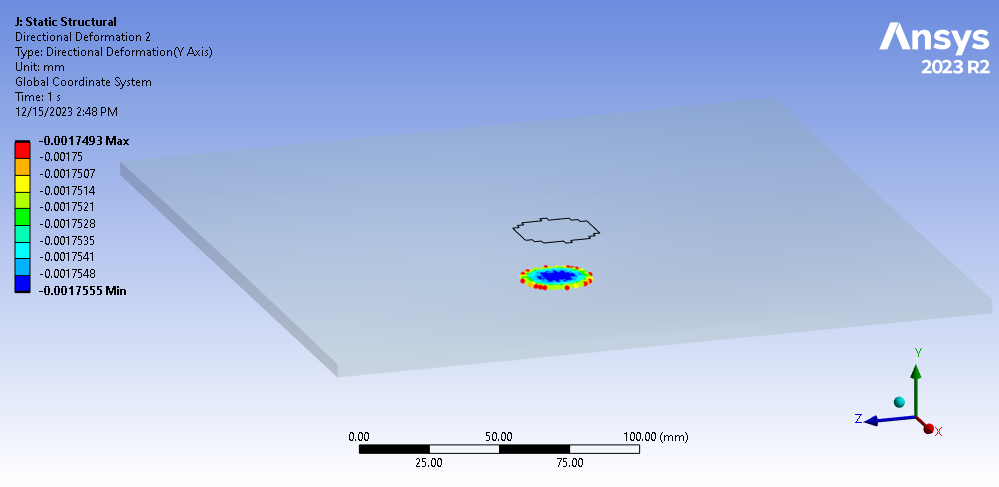
Figure 3: Deflection Results of Nodes Below Rod on Plate
ANSYS Mechanical provides this average directly from the Details of this result, and this average equals -1.7533e-003 mm. Therefore, the directional stiffness of our plate is: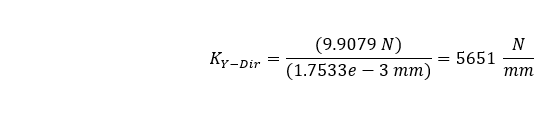
This value is significantly lower than that of the shaft and it is expected to dictate the duration of the impact period.
When performing a modal analysis, one should keep in mind that at the time of impact, the mass of the plate will be joined by the mass of the cylinder, therefore, the modal analysis will need to consider both of these components, which produces the following results.
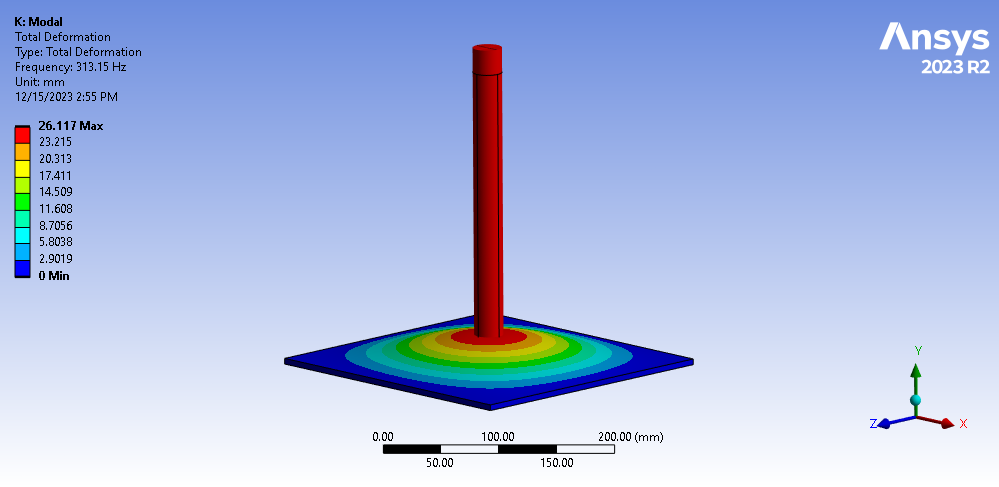
Figure 4: Modal Analysis Results of Combined Plate and Cylindrical Rod Model
With the natural frequency calculated at 313 Hz for the mode shape aligned to the impact direction, the period of the transient analysis can be calculated as follows:
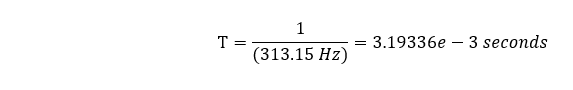
We know from Part 1 of this series, that we can expect accurate assessment of both deflections and stresses if we consider 128 time steps during the solution... but this is based on the period associated with the natural frequency of the bar. The period associated with the natural frequency of the plate is much longer. Can we expect to achieve the same quality of results if we consider this number of time steps for this longer period? Let's see.
We define surface contact between the bottom faces of the bar and the top face of the plate and impose the 4428 mm/sec velocity on the bar as an initial condition, as we calculated in Part 1 of this series, representing a drop of our bar from a distance of 1 m before impacting our plate.

Figure 5: Transient Structural Model with Initial Velocities Applied to Cylindrical Rod
Running our transient structural analysis shows the instant for which maximum deflections occurs in the plate while impacted by the cylindrical bar.
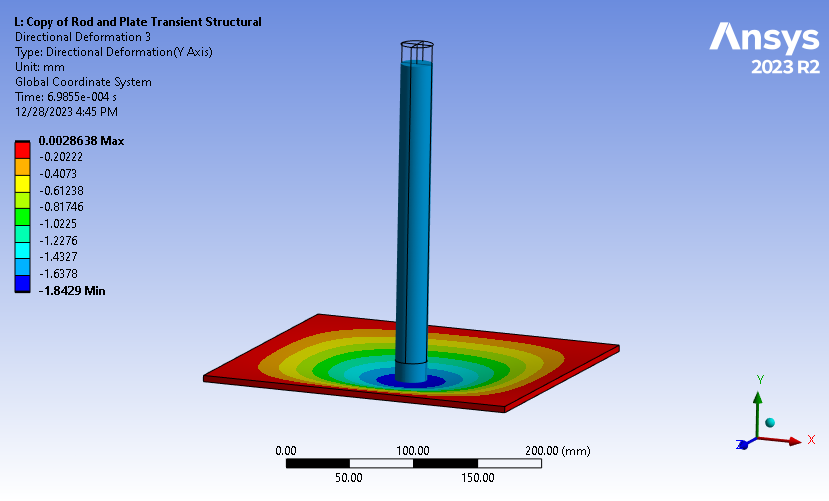
Figure 6: Maximum Deflections from Transient Structural Analysis While Considering 128 Time-Steps
If these deflections are plotted over time, they will appear as follows:
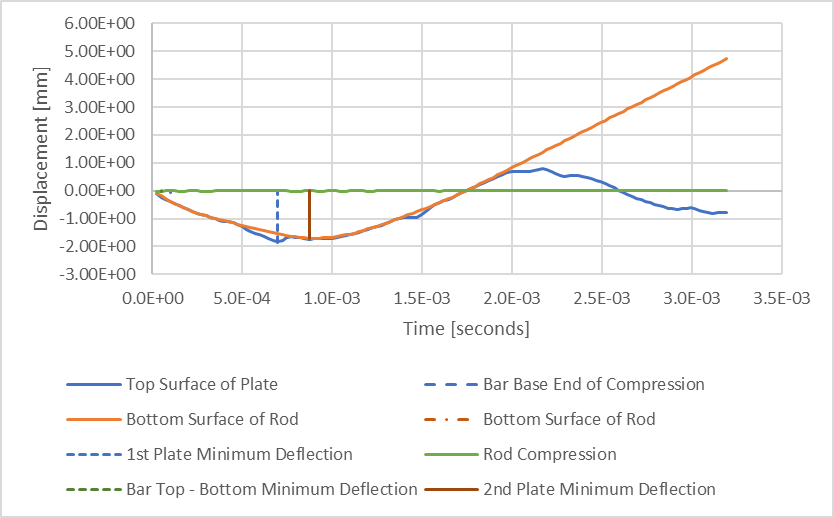
Figure 7: Deflections Plotted Versus Time While Considering 128 Time-Steps
Here we see the bottom surface of the rod (orange) has a gentle parabolic shape, while the top surface of the plate (blue) has a more complex response and seems to be bouncing with the bottom of the rod during impact. The green line represents the compression of the rod, which seems very small (-0.03187 mm) relative to the deflection of the plate (-1.8159 mm). Showing the plot of only this rod compression verifies these observations.
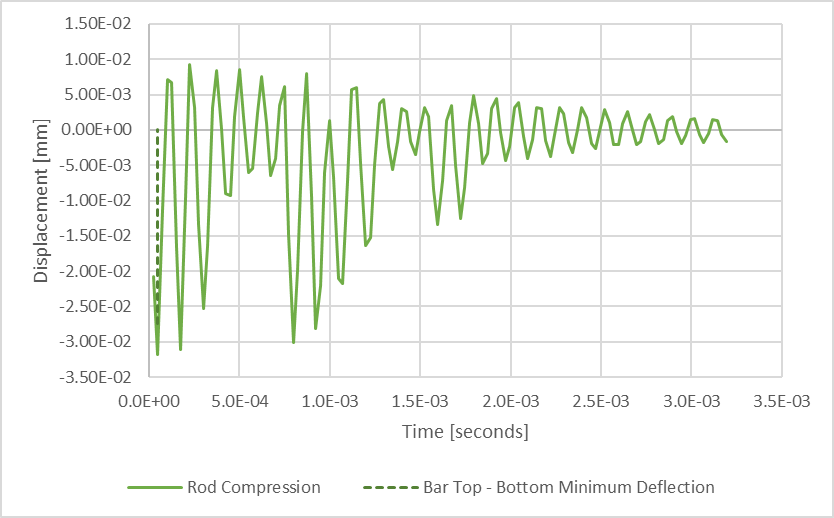
Figure 8: Rod Compression Plotted Versus Time While Considering 128 Time-Steps
It should be obvious that using 128 time steps resolved the plate deflections very well, but the response of the rod compression may be under-represented using this capture rate. If we were to consider the natural frequency of the rod to determine the capture rate, then we might expect to require 2030 time steps for this duration.

Changing analysis settings to utilize 2030 time steps instead of 128, means that the analysis will likely take 16 times longer to solve, and generate proportionally larger result files as well. To reduce the cost of our hunch, let's instead consider half this number of time steps, which suggests 64 time steps per rod natural frequency period and will solve in half the time. Therefore, reanalyzing the same model but utilizing 1015 time steps produces the following results.
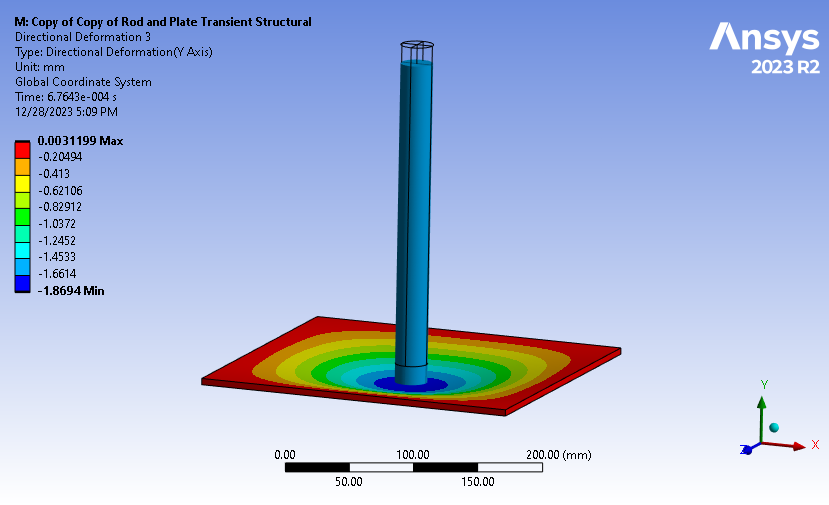
Figure 9: Maximum Deflections from Transient Structural Analysis While Considering 1015 Time-Steps
Producing a maximum deflection of 1.8694 mm, these results are only 1.4% larger than were produced while considering only 128 time steps. Plotting these deflections vs time shows greater resolution to the dynamic response of the plate as it bounces away and against the bottom of the rod during the rod's parabolic deflection path.
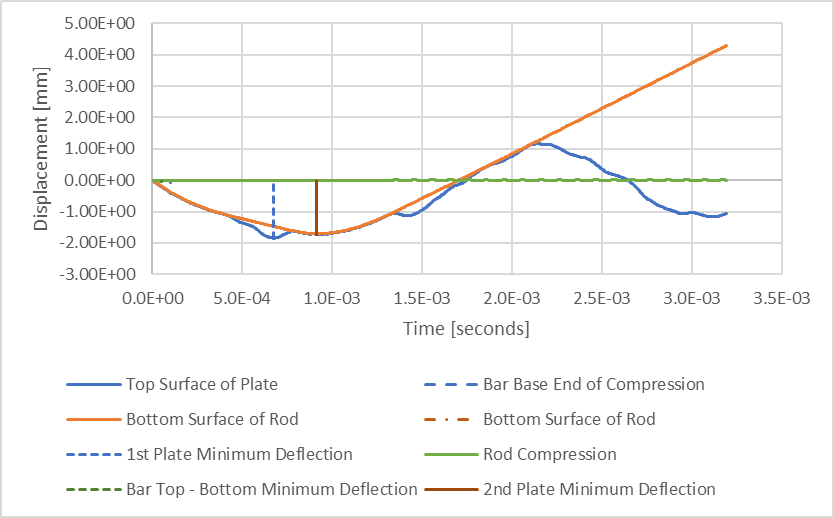
Figure 10: Deflections Plotted Versus Time While Considering 1015 Time-Steps
Closer examination of the rod compression shows much better resolution while considering 1015 times steps.
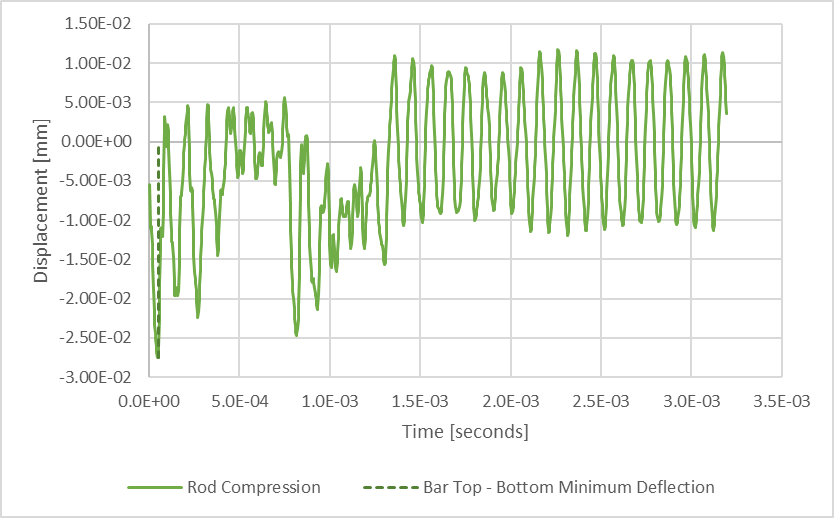
Figure 11: Rod Compression Plotted Versus Time While Considering 1015 Time-Steps
Is this analysis effort justified if we only achieve a 1.4% change in maximum deflection magnitude of the plate? The answer will relate to where are the results of interest. If our goal is the understand the deflections of the plate, then utilizing 128 time steps will be sufficient. Conversely, if we are interested in the response of the rod as it impacts our plate, then we will need to adjust the time stepping to accommodate the rod dynamics... which would suggest 1015 time steps, or more, for this particular scenario. But there is more we can learn from this comparison.
Examining our deflection plots, we see that the maximum plate deflections are identified with a dashed blue vertical line, which occurs at an earlier time that the maximum downward displacement of the rod's bottom surface. We have identified a 1.4% difference in these displacement results while comparing the 1015 time step analysis results to those produced while considering 128 time steps. If we focus on those maximum deflections of the plate near those maximum downward displacement of the rod's bottom surface, we find that the difference in displacement are to within 0.5% between these two analyses.
| Number of Time Steps | Bottom Surface of Rod Displacement [mm] | Top Surface of Plate Deflection [mm] |
| 128 | 1.7134 | 1.7357 |
| 1015 | 1.6981 | 1.7264 |
Figure 12: Table Listing Maximum Deflections Per Part
Based on these observations, we can establish that if our goal is to understand the general deflections of our softer component (plate) in our impact problem, we can achieve adequate results while considering 128 time steps only and still uncover important details of that component's more complicated dynamic response as well. If our focus is to understand more about this complicated dynamic response, then we can utilize additional time steps, but recognize that the response may not be significantly different.
Let’s compare our finite element deflection results to our hand calculation by equating our Potential Energy of our falling cylinder with Elastic Energy or our flat plate.

In this case, we will need to ensure proper units:
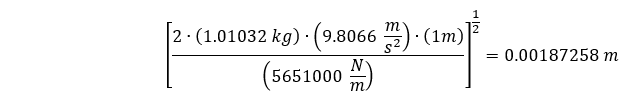
Therefore, our theoretical maximum deflection of the plate should be about 1.87 mm, but our analyses show 1.74 mm @ 128 time steps and 1.73 mm @ 1015 time steps, which is a difference of 7.3% and 7.8% respectfully.
If we consider the maximum downward deflection of the plate during any time of the event, then we acknowledge 1.82 mm @ 128 time steps and 1.85 mm @ 1015 time steps, which is a difference of 3% and 1.4% respectfully. However, I am not inclined to think that our hand calculation is considerate of complex vibrational response of two flexible bodies and therefore focus more on the former comparison rather than the latter.
As a final check, we can measure the time associated with the impact for these two scenarios, as the time it takes before the plate surface reaches its original position. The duration of impact is reflective of ½ the period of its natural frequency in the direction of compression. Therefore, the following should be true.

Therefore:
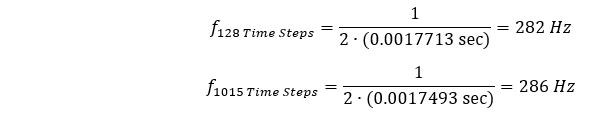
By either measure (282 or 286 Hz) at best, we are about 9% different than the expected impact duration associated with our estimated impact frequency of 313.15 Hz. These results show that our method to estimate the duration of the impact event and its associated capture rate is still reasonable, but less perfect as we include additional flexible participants in the event.
Of course, we crave to view the dynamic stress results, which appear as follows:
Figure 13: Animation of Transient Structural Impact Stresses While Considering 128 Time-Steps
Figure 14: Animation of Transient Structural Impact Stresses While Considering 1015 Time-Steps
Plotting these maximum stresses over time for both time-stepping schemes illustrates how these peak stresses differ.
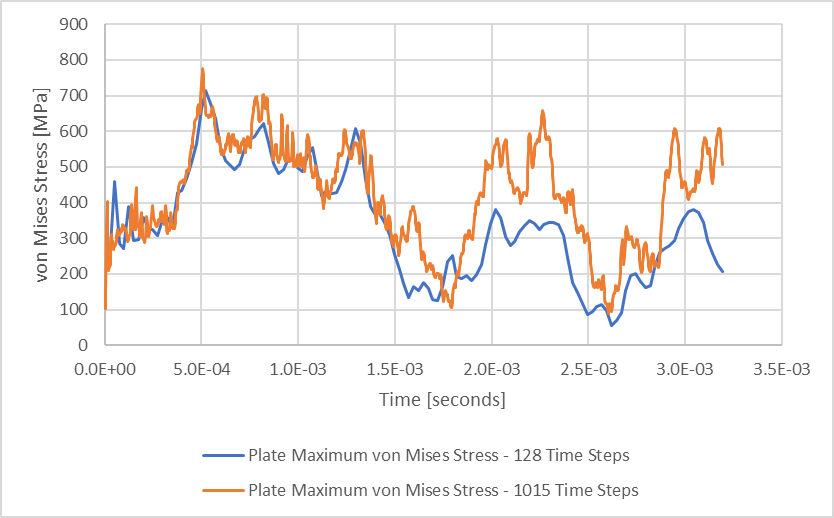
Figure 15: Maximum Plate von Mises Stress Plotted Versus Time
The general trend of peak stress is captured while using 128 time steps for our event, but the 1015 time-steps reveals higher frequency oscillations which are filtered from the analysis using fewer time steps. In either case, the peak stress is 714 MPa while considering 128 time steps and 776 MPa while considering 1015 time steps.
Conclusion
While exploring the transient analysis of the impact of a cylindrical rod onto a more flexible plate, we confirm that our method to determine the analysis duration based on the natural frequency of the more flexible of the two components is satisfactory. Also, we confirm that utilizing 128 time steps during this duration still produces maximum deflection results to within 7.8% difference compared to classical hand calculations based on energy equations. We did find that we could produce more detailed results solving with more time steps, but at the expense of longer analysis times and larger result files. The difference in maximum deflections was only 1.4% and the difference in maximum stress was under 8% while considering 1015 time steps instead of 128.
Part 3 of this series will consider our cylindrical rod as it impacts another cylindrical rod of the same stiffness so that we complete our understanding of the analysis settings of event duration and time-step size for transient structural analyses.
Tags:
Time-Step Frequency, Impact, Potential Energy, Elastic Energy, Static Structural Analysis, Kinetic Energy, Impact Velocity, Impact Period, Natural Frequency, Transient Structural Analysis, Analysis Duration, Displacement, Stress, ANSYS Mechanical
Dec 29, 2023 4:37:44 PM
