In this blog I demonstrate how to compute winding inductance using Flux Linkage and Current results from the Magnetic Transient Solver in Ansys Maxwell. The Ansys Maxwell Magnetic Transient Solver considers Eddy Effects in the calculations of the fields, and I will show an easy method to compute winding inductance using the results of Flux Linkage and Current.
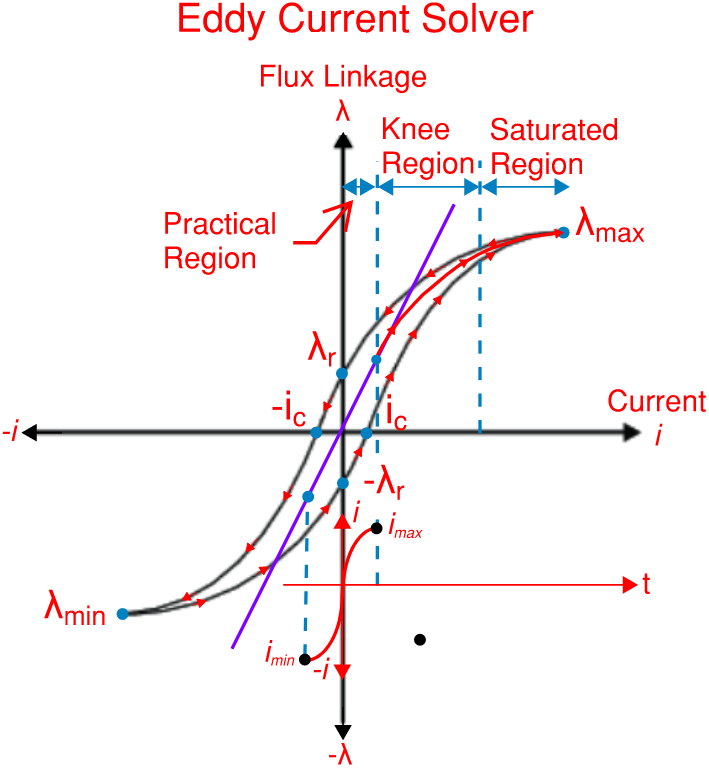
Inductance in reality is non-linear, depends on frequency and temperature. The incremental (differential) inductance is the actual inductance at a given frequency, operating point, and temperature. The inductance of the winding first changes along the magnetizing curve, starting from zero current and flux, and then changes around the hysteresis loop. In the region before the "knee" of the magnetizing curve (the practical region in transformers and rotating machines), the apparent inductance can be used to approximately linearize the inductance, and simulators would give reasonable results, depending on the application. After the "knee" of the magnetizing curve, in the saturation region, linearizing inductance would not yield accurate results in simulation. Sometimes airgaps are used in cores to linearize the inductance but this would reduce the flux for a given mmf without the airgap and higher winding losses would incur.
Many useful engineering applications do not need a non-linear model if the linear model is good enough. What is the acceptable error in the application is a question that should be considered and answered.
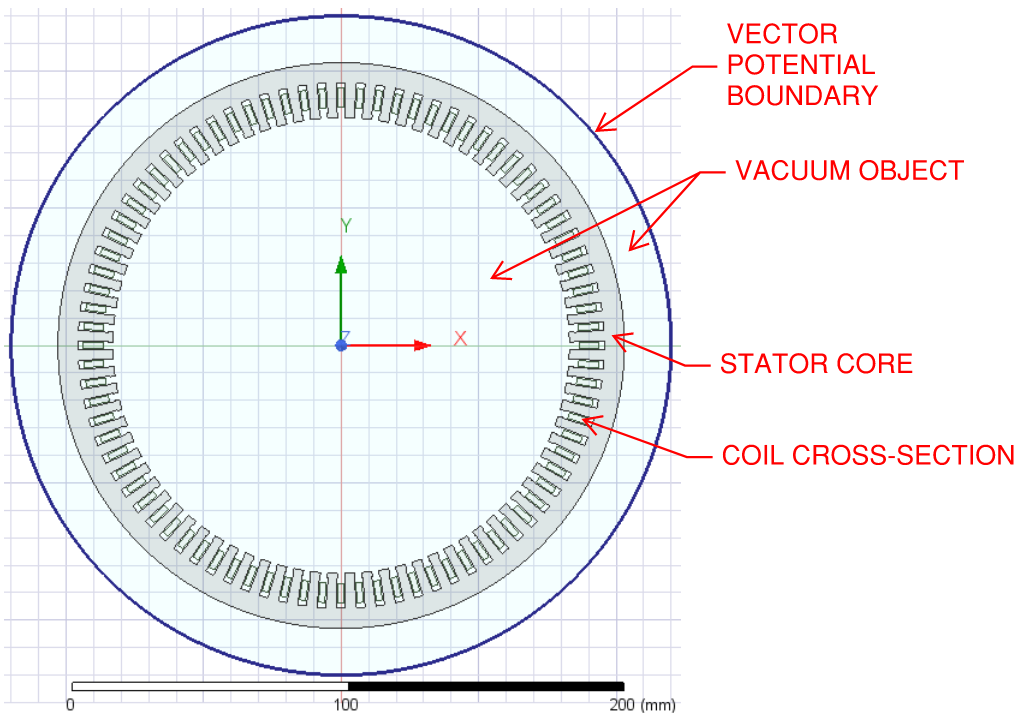
MAXWELL MODEL
Mesh operations were applied to the core to obtain accurate results. Three phase sinusoidal excitation of one amp was applied to the windings. The time step used was the electrical period divided by 1000.
MAGNETIZING CURVES AND HYSTERESIS LOOPS
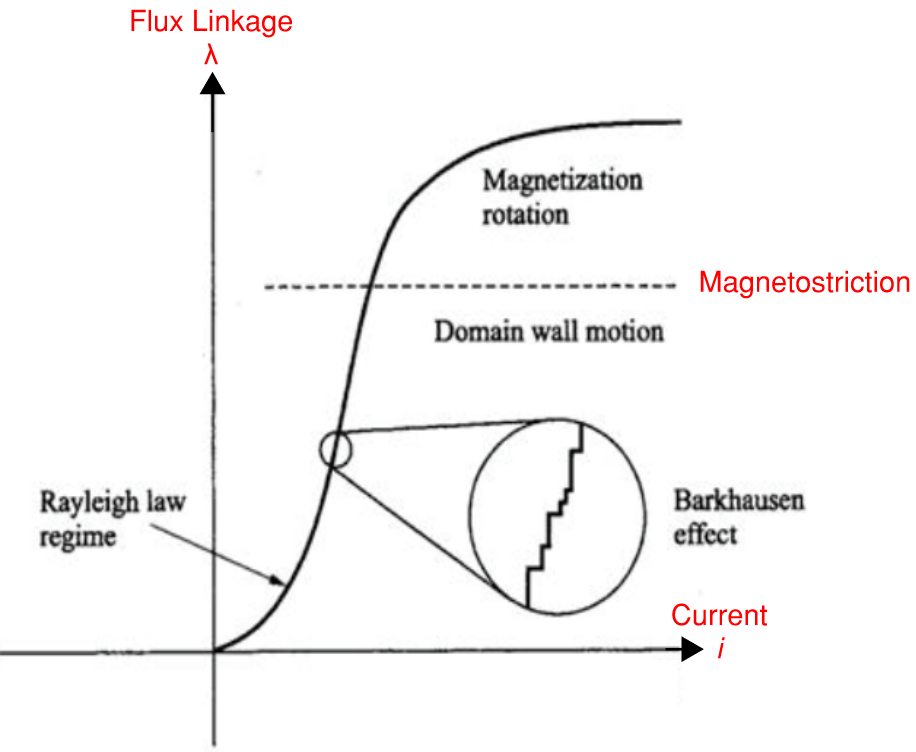
The magnetizing curve of a non-linear magnetic material is developed by applying excitation starting from zero excitation and increasing in one direction, say the "positive" direction, up to a maximum point in the saturated region where the slope equals inductance with air core. Magnetizing curves can be represented with a Flux Linkage and Current relationship or with a Magnetic Flux Density and Magnetic Field strength relationship and both relationships are directly related, and are scaled versions of each other. Both curves have the same shape and characteristics.
The magnetizing curve can be divided into three distinct regions as follows:
(1) Practical Region: optimum performance where inductance is high for a small excitation current, winding loss is low, and induced voltage, current and torque is high.
(2) Knee Region: performance declines and inductance decreases.
(3) Saturated Region: inefficient performance where inductance is equal to inductance of an air core inductor. Applying a large increase of current excitation is not justified because it does not result with a large increase of Flux Linkage gain as in the practical region, and winding loss is increased with current squared. Also, a saturated core contributes to higher harmonics in the winding currents and air gap flux density (rotating machines), noise (humming) and vibration in the core due to the Barkhausen effect and magnetostriction, and harshness which is associated with noise and vibration.
Magnetostriction is the change of volume of a saturated core as the magnetic domains walls expand to allow and domains alignment of the domains with the applied field. The domain walls boundaries expand (domain wall motion) or change structure (magnetization rotation). The Barkhausen effect is due to rapid change of magnetic domain alignment and is stronger in the saturated region and the figure below shows the magnetizing curve is not smooth.
Magnetostriction is not desired in rotating machines and transformers. However, some actuators and transducers use magnetostrictive material to convert magnetic energy into kinetic energy.
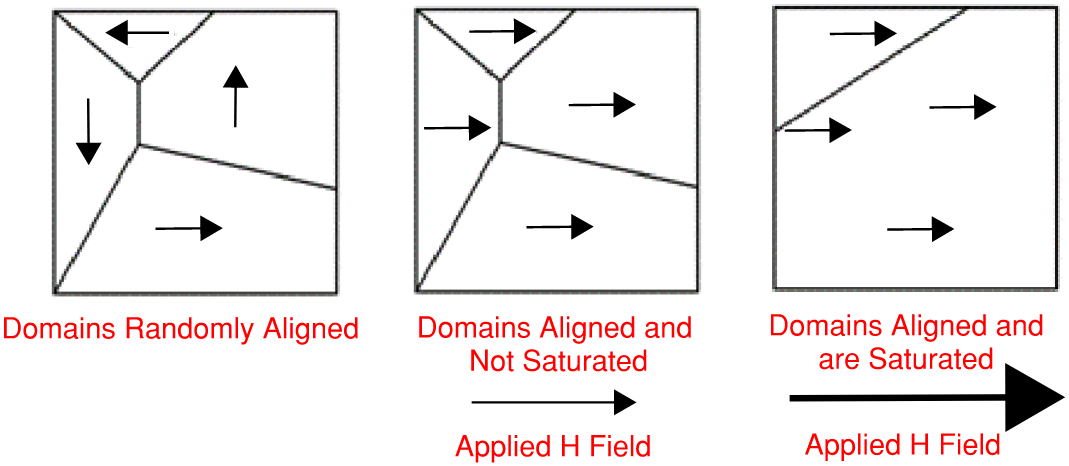
Magnetic wall boundaries divide the magnetic structure into domains where magnetic dipoles in each domain are aligned in the same direction, while magnetic dipoles are aligned in other directions in other domains. When a magnetic field strength H, function of current, is applied to a magnetic material, the magnetic field permeates the material and aligns all the magnetic domains in the direction of the applied field. In the non-saturated, practical region, the magnetic domain wall boundaries expand and contract as the applied field changes direction and the domains are realigning with the applied field, but the structure of the wall boundaries does not change significantly. However, under saturation the structure of the magnetic domain wall boundaries changes (reshapes) significantly, or boundaries are removed during the alignment of the domains with the applied field (larger than necessary and without benefit).
The magnetizing curve does not follow the same path when the current is reversed at any operating point because the magnetic material has "memory", and this phenomena is called "Hysteresis". Flux Linkage remains, "Remnant Flux", in the core after the excitation is brought to zero from one direction. Applied current excitation, "Coercive Current", in the opposite direction is required to bring the flux to zero.
The deviation from the original path is smallest in the practical region (smallest losses) and largest in the saturated region (largest losses). Magnetic material contribute to power losses equal to the area of the loops formed by hysteresis over one period of excitation.
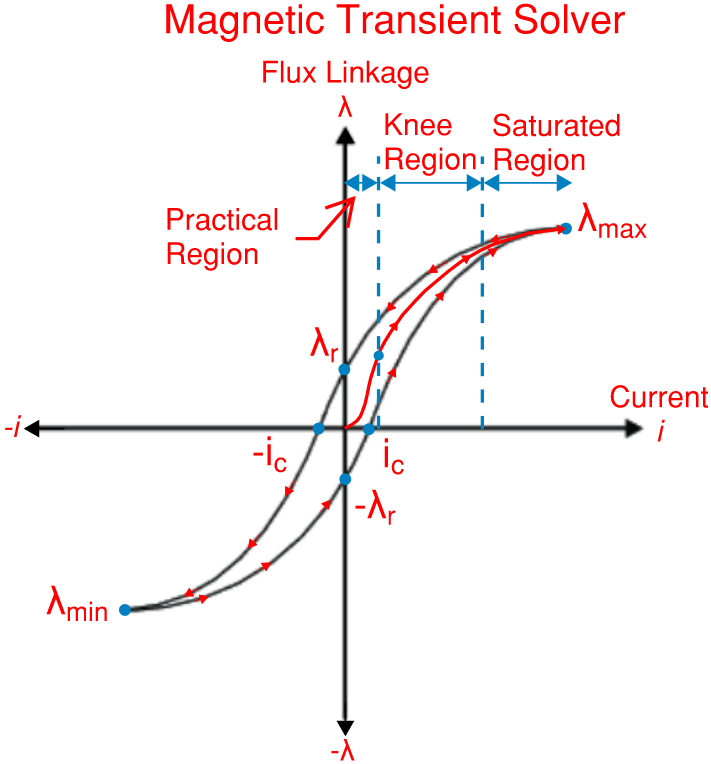
The apparent inductance at the operating point is used to linearize inductance in the Eddy Current solver, and in general in any other frequency domain, steady state solver which use AC waveforms. There is only one inductance in this type of solver, while in the Magnetic Transient solver there is also incremental inductance.
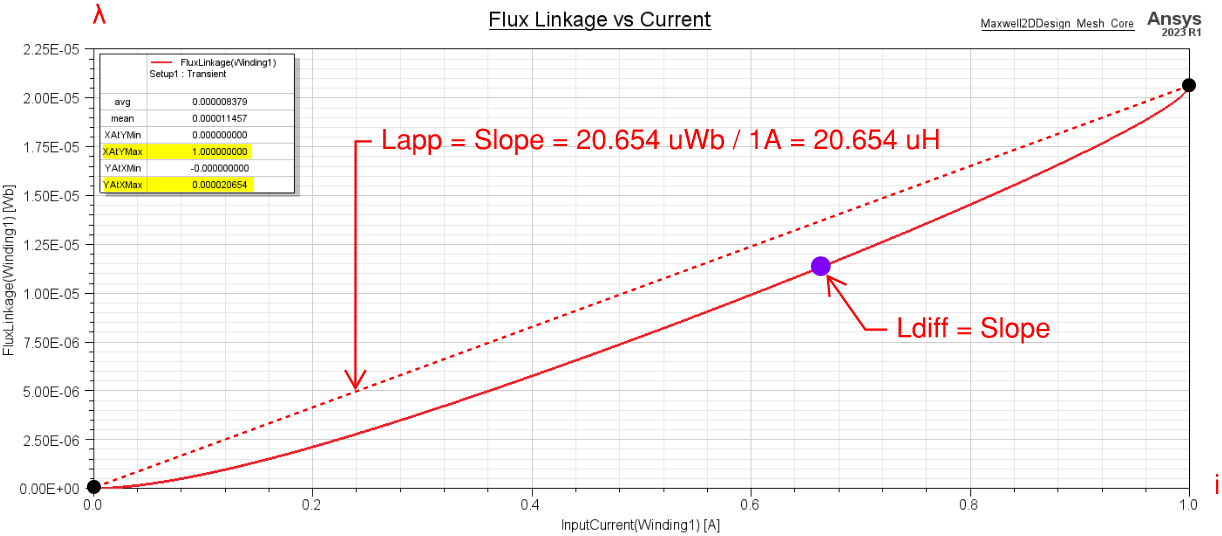
FLUX LINKAGE vs CURRENT
Flux Linkage vs Current (from zero to maximum) is plotted below. The apparent inductance is equal to the Flux Linkage divided by the Current with respect to the maximum operating point.
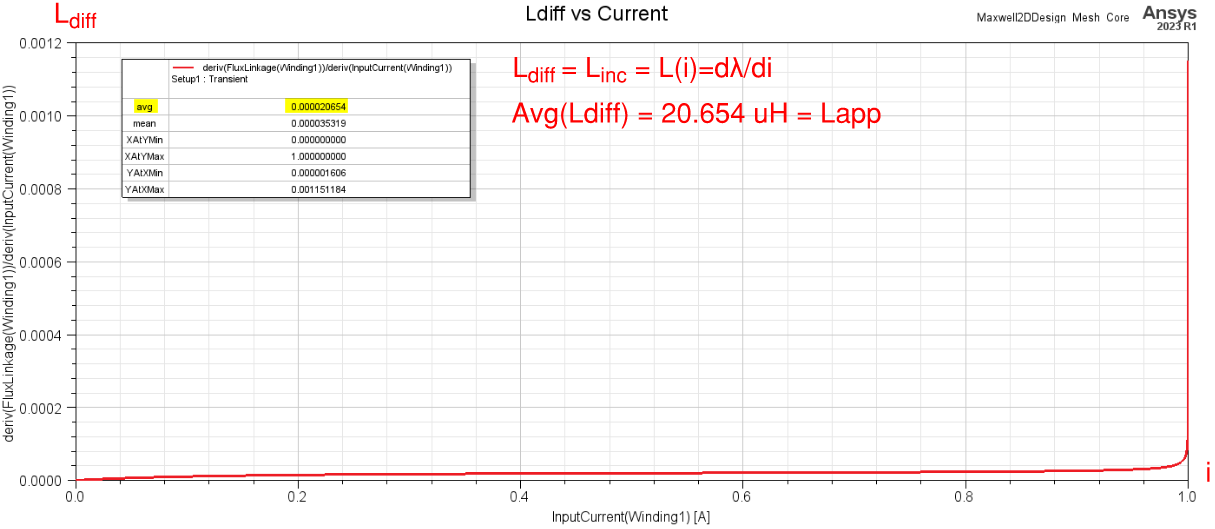
INCREMENTAL INDUCTANCE VS CURRENT
The incremental inductance, or differential inductance, is the derivative of the Flux Linkage vs Current plot. We see in the results below that the average incremental inductance equals the apparent inductance.
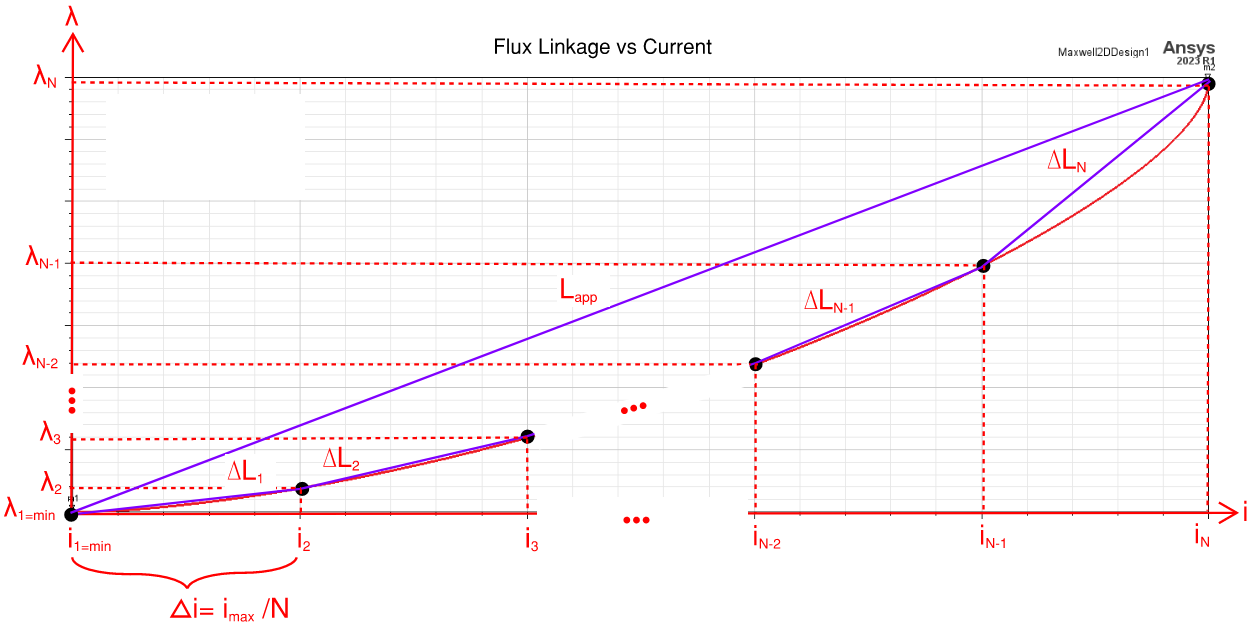
FLUX LINKAGE vs CURRENT - ANALYSIS
Below is an analysis showing how the average of the incremental inductance equals the apparent inductance.
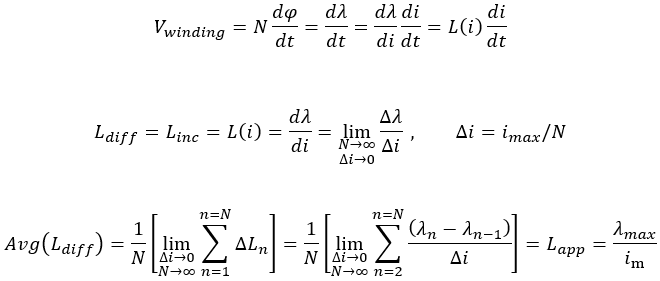
That is all for this blog. You may leave a comment or question and I will try to respond.
Contact us at Ozen Engineering Inc. to inquire about our services and learn how we can help you with your engineering projects.
Please check out the video associated with this blog:
ABOUT OZEN ENGINEERING INC.
Ozen Engineering is a leading provider of Ansys solutions, catering to a diverse range of industries with a specialization in electronics, semiconductor, biomedical, healthcare, aerospace and automotive applications. Our team delivers personalized solutions to optimize product design and performance by seamlessly integrating Ansys simulation into the product development process. As an elite channel partner of Ansys, we provide best-in-class software tools, consulting, training, mentoring, and technical support.
Contact us to learn about our simulation capability and request a demonstration for us to show you how we can help you with your engineering projects. Ozen Engineering Inc is an Ansys Elite Channel Partner, and we provide training to use Ansys tools, offer consulting services, and sell Ansys software packages.
Visit our website
Give us a call
Send us a message

Apr 26, 2023 6:29:54 PM
